引用本文
冯仁丰. 分析误差概念的更新. 2012, 27(11): 979-983
  
Permissions
Copyright©2012, 《检验医学》编辑部
《检验医学》编辑部
分析误差概念的更新
冯仁丰
上海市临床检验中心,上海 200126

作者简介:冯仁丰,男,1942年生,主任技师。

摘要

近期,国内正在推出正确度核实等的质量评估工作。但是,基层大多数临床实验室人员对什么是正确度还不理解。说起检测质量就会讲到2个方面:精密度和准确度。怎么现在要讲正确度了?其实,正确度不是什么新词语,只是在临床实验室习惯讲的是准确度,我们从来没有注意和重视正确使用“准确度”。本文就3个关键分析性能词语——准确度、正确度和精密度的正确含义作如下介绍。

关键词: 分析误差; 准确度; 正确度; 精密度
中图分类号:R195.1 文献标志码:A 文章编号:1673-8640(2012)12-0979-05
on the performance of creatinine testing system in China
Abstract
Keyword:

自21世纪以来, 临床检验的标准化倍受国际化标准化组织的关注。国际标准化组织(ISO)的ISO 9000系列文件[1, 2, 3]和专为临床检验管理起草的标准化文件已有多个[4]。按照这些文件对误差类型的定义和应用, 已经深深地影响着临床检验界对质量管理的认识。我国新的文件中也已经引用了这些词语的定义。

首先出现正确度的是美国临床实验室标准化协会(CLSI)于2005年发布的EP15-A2文件(User verification of performance for precision and trueness— second edition)[5]中, 将原先版本中该文件标题“ 用户对精密度和准确度(accuracy)性能的核实” 改成现在的“ 用户对精密度和正确度性能的确认” 。这是什么原因?

一、临床实验室对于误差的理解和估计的表达[6, 7, 8]

1. 针对临床实验室对每个样品只做1次检测的做法, 在对检测结果具有的误差进行估计时, 我们还是采取对某样品多做几次检测的做法。

2. 假定所有检测结果呈正态分布, 则可以用均值表示所有结果的集中趋势, 以标准差表示所有结果对于均值的离散程度。

3. 对于误差的分析。将均值与参考值的差视为不准确度, 以偏倚表示, 为系统误差。实际的做法是:确认某种方法可靠, 在评估某新方法的可靠性时, 对一组患者样品进行方法学比较, 比较2种方法检测结果的均值差异为不准确度的大小, 即偏倚。这是以确认的方法结果为准, 被评估方法相对于确认的方法在均值浓度下具有的不准确度。以重复检测某患者样品, 以均值为准, 2s表示该检测系统(方法)对于样品浓度在均值下各个检测结果对于均值的离散分布可能性, 即不精密度, 为随机误差。然后依据正态分布规律, 将相同分析物浓度下的偏倚+2s表示为该浓度下单次检测具有的总误差(TE)。

4. 问题有:(1)通过方法比对实验来确定各个样品检测结果的均值和他们的理想总均值(靶值)的差异确定为该检测系统在样品均值浓度下的不准确度, 是系统误差的表现, 称为偏倚。这个说法与准确度的定义是否有矛盾?(2)TE究竟是什么?当今, 提出准确度和正确度的概念, 与TE的关系是什么?(3)为什么要提出正确度?其意义究竟是什么[9]?

二、被测量和真值
(一)被测量(measurand)的定义

作为测量对象的特定量[VIM:1993, 2.6]。在测量中, 为完整地表述被测量之值, 使其具有较严格的单一性, 必须把影响被测量之值的量(当然也影响测量结果)加以说明。也即对被测量要有明确的定义。

随着人类对自然的深入认识, 被测量已经变得非常重要。因为当我们去描述某个检测系统的可靠性时, 我们讲精密度、正确度和准确度, 究竟是哪个检测“ 对象” 的性能?不清楚被测量, 所有的性能估计毫无意义。

例如, 血清双缩脲总蛋白测定, 被测量是总蛋白。正因为体内的蛋白类型之多, 至今还无法说清楚。但是, 临床希望大致了解患者蛋白含量, 双缩脲总蛋白测定对人体血清内蛋白总量具有较好的量值估计。所以, 可以将总蛋白作为被测量。

又如:肌酸激酶同工酶MB(CK-MB)测定。目前有2种检验技术, 得到不同的CK-MB结果。血清CK-MB酶催化活力测定; 血清CK-MB免疫酶蛋白量测定(后者至今被称为mass测定)。这是2个不同的被测量。

今天, 随着对事物的深入研究和了解, 知道“ 生物标志物” 检测的各类蛋白、核酸、酶类等“ 分析物” , 其实都是一个“ 大家庭” 。我们检测的对象从名词上一样, 但不同检测系统对样品检测“ 相同” 的项目, 却是不同的“ 被测量” !

一定要注意, 没有严格的被测量的定义, 或没有完整的检验项目名称, 就无法了解我们谈论的准确度、正确度、精密度或引入的误差究竟是属于谁的。

(二)真值

量的真值[true value(of a quantity)]定义:与给定的特定量的定义一致的量的值[VIM 1.19]。这个定义与原先定义有了原则上的改变。过去的定义中, 强调了完善测量所得到的量值。但是这种“ 完善” 永远是不完善的, 随着技术进步、认识的深入等, 原先以为是十全十美的测量, 又发现了缺陷。这样的过程是无尽的。因此, 真值只是理想的概念, 通过测量是不可能获得真值的。

另一个对真值描绘的词语为被测量之值。他就是人们心目中追求的“ 真值” 。但是, 通过定义使量值完全符合定义, 这样的值就成为真值了。例如, 电磁波在真空中的传播速度C0=299 792 458 m/s是按照定义确定的, 就是真值。

(三)约定真值(conventional true value)

临床检验的各个被测量(检验项目)均没有现今已经具有明确定义的真值。约定真值的定义为:对于给定目的具有适当不确定度的、赋予特定量的值, 有时该值是约定采用的[VIM 1.20]。这是目前绝大多数在估计正确度和准确度赖以比对的“ 真值” 。

在临床检验中讨论以下的准确度、正确度时, 均采用了目前被称为约定真值或较之更低的可接受参考值, 为目前理解的“ 真值” 。

三、正确度和偏倚

准确度的完整表达应是检测准确度(accuracy of measurement), 其定义为检测结果与被测量真值之间的一致程度[VIM 1001-1998, 定义5.5]。不论临床实验室的检测结果是对样品仅作一次检测就报告的, 该结果的准确度就是这个检测结果与真值的一致性, 称为准确度。度量准确度的是不准确度。

那么按照前述, 我们在评价检测系统的不准确度时, 是对多个样本进行方法比对实验, 结果是观察2个方法的均值的差异大小度量为不准确度[注意:这里是均值间的比较!但是, 在这里的不准确度的概念是:检测结果与某真值(可以是参考值或可信方法值)的不一致性, 两者有着显著的不同]。

引出正确度是解决困惑的关键。在ISO的标准化协调下, 依然保持了准确度的定义。但是, 方法学比较的均值间一致性引出了“ 正确度” 概念。

(一)正确度

正确度的完整词语为检测正确度(trueness of measurement), 其定义为大批检测结果的均值与真值的一致程度。正确度的程度通常用与正确度相反的统计量“ 偏倚” 表示, 是检测结果的期望值与被测量的真值之差(也即为不正确度的度量)。

因此, 长期以来我们认为的准确度, 应该是正确度, 其客观地表达了我们以多次检测均值与“ 真值” 比较的性能评估做法。

(二)系统误差(systematic error)

系统误差的定义:在可重复的条件下, 对同一被测量无限多次检测结果的均值, 与被测量真值的差异[VIM 3.14]。可以表达为系统误差= x̅∞-Xo。式中X0为被测量, 这里用以表示真值。很明显, x̅∞只是真值与系统误差的代数和, 其差自然是系统误差。

注意:(1)系统误差=误差-随机误差; (2)系统误差并不属于某个检测结果xi, 在同一条件下的各个检测结果均具有相同的系统误差值; (3)由于真值X不能通过检测获知, 系统误差也只能通过有限次数的平均值 x̅与X的约定真值近似地得出, 是系统误差的估计; (4)与真值相似, 系统误差和其原因不可能完全了解。表示系统误差大小的统计量为偏倚。

(三)偏倚

偏倚的完整词语为检测偏倚(bias of measurements), 定义为检测结果的预期值与可接受值间的差异[ISO 3534-1, 1993]。一般情况下, 使用可接受的(确定、参考或设定的比较)方法和被评价的方法, 各自对样品的重复检测间的离差/差异, 以检测计量单位或百分率表示, 即均值与参考值的差异。

(四)正确度与偏倚

正确度和系统误差的定义都指出评估检测不正确度时均使用重复检测结果的均值。因此, 这些均值对于真值、参考值或某设定的比较方法结果均值间的差异, 即偏倚就成为估计的误差量。

了解分析过程的正确度, 必须在去除了检测中不精密度后的检测均值, 以其和可以接受的值(真值)比较的偏倚, 说明不正确度的大小, 以此度量正确度是最可靠的。偏倚使检测结果偏高或偏低, 有一定的大小。这类误差有一定的方向和大小, 故称为系统误差。有系统误差的结果是不正确的。

四、准确度和误差
(一)准确度

准确度定义为检测结果与被测量真值间的一致程度。正确度的定义为大批检测结果的均值与真值的一致程度。2个定义使检测结果与真值比较的做法不同。

准确度:检测结果直接与真值比较。

正确度:检测结果均值与真值比较。

因为临床实验室对每个样品只做1次检测就发出报告。因此, 单次检测很不可靠。要知道准不准或正确不正确, 唯一的做法是用多次检测的均值与可靠的参考值(真值)比较。

根据ISO 5725-1, 检测准确度与检测的正确度和精密度有关。这也指出了在临床实验室对样品的单次检测, 只有知道了不精密度和不正确度后, 他们的估计误差之和才是对不准确度(即准确度)的估计。就被测量而言, 准确度不能给出一个数字形式的值, 只能根据一个明确的目的描述为“ 足够” 或“ 不足” 。

1. 准确度定义说明没有检测(测量)就无从说起准确度, 所以其在定义上完整的表达为检测准确度。
2. 与真值的一致程度, 在实际使用中难以度量。首先是真值是什么?在哪里?以前只在定义上使用, 而无具体化。近年来提出使用“ 可接受参考值” , 这可以是理论值(真值)、赋值、公认值或由程序确定的值。现在, 临床检验重视论述检测系统对患者样本的检测结果的溯源性。如果检测系统说明其检测结果可以溯源至国际公认的参考物质或参考程序(方法), 那么这个参考值就不是空虚的, 而是实在的。
3. 不准确度是检测值与真值的数量上的差异。
(二)检测误差(measurement error)

简称为误差, 即检测结果与被检测(测量)值的差, 或检测结果减被测量之值[VIM; ISO 3534-1, 1993]。依据定义, 误差值可正可负, 检测结果大于真值时为正, 小于真值为负。

以上2个词语含义相同。均说明凡是检测结果对于真值或可接受参考值的偏离或差异, 这就是“ 不准确” 。检测准确度的好坏确实是以不准确度来度量的。

由于真值不能确定, 误差也只能通过约定真值近似地评定, 称为误差的估计。误差往往由若干分量组成, 其合成只有一种形式, 即各误差分量的代数和。

如果把这些分量分为随机误差和系统误差[VIM 3.13], 则误差即是这2类误差的代数和, 也即测量结果等于真值加随机误差加系统误差。因此, 上述不准确度度量的就是检测结果的误差。

失误(差错)不应视为误差。

报告结果时的“ 准确度” 的好坏, 实际上就是以估计总分析误差的方式, 用“ 不准确度” 予以度量。也即平时我们习惯的总误差估计, 实际上是对检测结果的不准确度的估计。

临床检验对每个患者样本只作1次测定时, 差异或偏离不仅包括检测系统分析过程的不正确度, 也包括了分析过程的不精密度。

即:不准确度 = 分析过程的不精密度+分析过程的不正确度。

也即:不准确度=TE=分析过程的随机误差+分析过程的系统误差。

五、精密度和标准差
(一)精密度

精密度的完整词语为测量精密度(precision of measurement), 定义为在规定条件下相互独立的检测结果间的一致程度[ISO 3534-1, 1993]。

检测精密度不能给出被测量的数值, 在指定目的下只能以“ 足够” 或“ 不足” 进行描述。

精密度的程度通常用与精密度相反的检测不精密度统计量表示, 如标准差和变异系数。

给定检测程序的“ 精密度” 可以根据特定的精密度条件进行分类。

(二)重复性(repeatability)和再现性(reproducibility)

“ 重复性” 与基本不变的条件有关, 常称为“ 序列内精密度” 和“ 批内精密度” 。

“ 复现性或再现性” 与条件改变有关, 如时间、不同实验室、不同操作者和不同检测系统(包括不同校准品和试剂批号)下的精密度。

随机误差=xi- x̅∞, 式中xi为被测量X的某一个检测结果, x̅∞为重复性条件下无限多次的检测结果的平均值。很明显, 由于xi等于真值、系统误差与随机误差这三者的代数和, 而 x̅∞等于真值与系统误差的代数和, 在 x̅∞中的随机误差为零。 因此, (1)随机误差必定随检测结果xi而异; (2)随机误差只对给定的检测结果xi, 而不存在对重复性条件下其他检测结果均适用的随机误差大小; (3)随机误差表示这样的差异以该均值下的标准差大小来度量; (4)无限多次的重复检测结果中的各不相同的无限多个随机误差的代数和必然相互抵消为零。所以随机误差的期望值为0。

在临床实验室对每个患者样品只做单次检测报告的情况下, 无法对该结果具有的确实随机误差作出测量, 只能“ 估计” 。以多少s可能具有的随机误差大小进行估计。

六、不准确度的度量

按照上述准确度内容, 对样品检测结果的准确度是以估计的不准确度描述的。原先我们熟悉TE的定义为:能影响分析结果准确度的确定误差的组合, 就是不准确度。

七、各个性能误差的关系

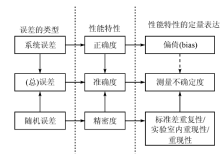
为了使大家对以上所述的各个性能误差有更加深入的认识, 在此引入Antonio等[10]的介绍。首先他们以图示方式表达误差类型、性能特性、性能特性的定量表达间的关系, 见图1。然后, 还写了以下很好的解释。例如, 随机误差对测量的影响表示为“ 精密度” 的性能特性, 可以在相同方法中对相同样品的重复测量的标准差予以量化。更详细的, 精密度可表示为:(1)重复性, 有最小的变化(例如相同的分析人员使用相同的仪器、在短期内进行的测定等); (2)实验室内重现性[within-laboratory reproducibility(intermediate precision)], 在相同实验室内各种相关影响因素的变异(例如对相同的样品由不同的分析人员、使用不同批号的试剂、在不同的环境条件下、在具有相同性能的不同仪器上进行较长时间周期的测定); (3)重现性, 应用于不同实验室的方法精密度(例如作为实验室间协调研究的一部分, 应用相同分析方案的各个实验室依据特定的统计设计进行的测定)。

图1 误差类型、性能特性和性能特性定量表达间的关系

相似的方式, 若一个或多个影响(influence)量造成对测量结果的影响, 被证实为误差的系统组分[系统误差], 这样的影响被性能特性表达为正确度。定量为偏倚, 即相同样品[如证实的参考物质(certified reference material)]多次测量的均值与其(常用)真值间的差异。这样的差异必须由相应的统计检验, 对偏倚测量的精密度与选择为参考的值的可靠性进行评估。所以, 实验精密度(作为均值的标准差)和参考值的不确定度是偏倚估计量的不确定度, 即使没有观察到明显的偏倚。

由于影响量的变异会以随机和系统的方式影响测量结果, 所以测量的定性性能特性— — 准确度包括了正确度和精密度二者, 正像水果的一般定义既包括苹果, 又包括桔子一样。正如水果和桔子的关系, 不可将准确度和精密度去替代正确度和精密度。

准确度是定性性能特性, 表示为测量结果和被测量值间的一致性。定量估计测量结果的准确度对于确定其可信度、并依据这样的结果作出决定的可靠性是必须的。这样的参数是测量的不确定度, 叙述了“ 值的离散, 并被适当地赋予被测量” , 常表示为标准差(标准不确定度)或包括这样值的较大组分的区间(扩展不确定度), 该区间由特定包含因子(k)乘以合成标准不确定度形成。已经提供的导则用于在评价测量不确定度时, 由重复性/重现性和正确度(偏倚)估计的二者信息[4, 5]。图1中的虚线箭头考虑偏倚组分对测量不确定度的影响。

虽然图1所示的构架还不彻底, 作者希望该图能提供一个简单和目视的方式, 激励进行讨论, 如何深入理解这些关联的基础概念, 以及他们应如何在分析领域中使用。

The authors have declared that no competing interests exist.

参考文献
[1] 质量管理和质量保证[S]. GB/T 6583-1994, 1994. [本文引用:1]
[2] 质量管理体系[S]. GB/T 19000-2000, 2000. [本文引用:1]
[3] International Organization for Stand ardization. Accuracy (truness and precision) of measurement methods and results-part 1: general principles and definitions[S]. ISO5725 -1 (1998), ISO, 1998. [本文引用:1]
[4] International Organization for Stand ardization. Guideline for the use of repeatability, reproducibility and trueness estimates in measurement uncertainty estimation[S]. ISO(2004) ISO/TS21748, ISO, 2004. [本文引用:2]
[5] Clinical and Laboratory Stand ards Institute. User verification of performance for precision and trueness-second edition[S]. EP15-A2, CLSI, 2005. [本文引用:2]
[6] Centers for Disease Control and Prevention, Centers for Medicare and Medicaid Services, HHS. Medicare, medicaid, and CLIA programs; laboratory requirements relating to quality systems and certain personnel qualifications. Final rule[J]. Fed Regist, 2003, 68(16): 3639-3714. [本文引用:1]
[7] Medicare, medicaid and CLIA programs: regulations implementing the clinical laboratory improvement amendments of 1988 (CLIA)—HCFA. Final rule with comment period of 1988 (CLIA)—HCFA. Final rule with comment period[J]. Fed Regist, 1992, 57(40): 7002-7186. [本文引用:1]
[8] Büttner J, Borth R, Boutwell J H, et al. Interna-tional Federation of Clinical Chemistry. Committee on Stand ards. Expert panel on nomenclature and principles of quality control in clinical chemistry. Approved recommendation (1978) on quality control in clinical chemistry. Part 1. General principles and terminology[J]. Clin Chim Acta, 1979, 98(1-2): 129F-143F. [本文引用:1]
[9] 冯仁丰. 临床检验质量管理技术基础[M]. 第2版. 上海: 上海科技文献出版社, 2007: 76-80. [本文引用:1]
[10] Antonio M, Marina P, Bertil M. Understand ing the meaning of accuracy, tureness and precision[J]. Accred Qual Assur, 2007, 12(1): 45-47. [本文引用:1]