作者简介:乐爱平,男,1971年生,学士,副主任技师,主要从事临床免疫学检验工作。
探讨血清乙型肝炎病毒(HBV)大蛋白(LP)浓度标准曲线的最适拟合模型,以建立并优化定量检测系统。
方法HBV-LP标准品吸光度( A)检测采用酶联免疫吸附试验(ELISA),对HBV-LP标准品浓度与 A进行四参数方程模型、线性模型、对数线性模型、二次多项式模型、三次多项式模型、S模型、Logistic模型的曲线拟合,并根据各回归模型决定系数( x2)的大小来确定最适拟合模型。
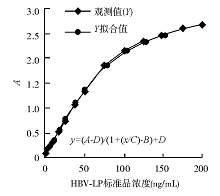
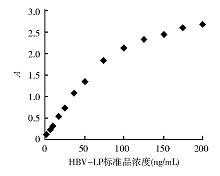
结果HBV-LP标准品浓度与 A的散点图呈非线性趋势;四参数方程模型、线性模型、对数线性模型、二次多项式模型、三次多项式模型、S模型、Logistic模型的回归方程均有意义( P<0.001), r2分别为0.999 5、0.924 9、0.876 5、0.997 5、0.998 9、0.979 9、0.864 7。其中四参数方程模型、二次多项式模型、三次多项式模型、S模型的拟合精度较好,以四参数方程模型最佳。
结论四参数方程模型是血清HBV-LP浓度标准曲线的最适拟合模型,这对血清HBV-LP浓度检测的建立及其检测准确度的提高具有重要的指导意义。
乙型肝炎病毒(HBV)大蛋白(LP)是从蛋白水平反映HBV感染者体内病毒复制程度的血清学新指标, 尤其是反映血清HBV e抗原(HBeAg)阴性和低水平HBV DNA的HBV感染者体内病毒复制、疾病进程、疗效与预后判断的敏感监测指标[1]。目前国内有少数几家临床实验室开始对血清HBV-LP进行定性检测, 而血清HBV-LP的定量检测尚未开展, 不能满足临床上利用血清HBV-LP浓度动态监测疾病进程的需要。为此本研究利用HBV-LP标准品进行血清HBV-LP浓度标准曲线拟合模型的优选, 分析出四参数方程模型是血清HBV-LP浓度标准曲线的最适拟合模型, 为临床实验室血清HBV-LP定量检测提供了理论依据, 有利于优化实验室检测系统, 提高血清HBV-LP定量检测的准确度。
1.HBV-LP标准品来源 由北京热景生物技术有限公司提供。利用昆虫杆状病毒细胞表达LP, 收集细胞, 加入0.1%十二烷基硫酸钠(SDS)裂解细胞, 电泳后扫描确定LP的含量, 而后采用含0.1%Proclin 300、4%牛血清白蛋白(BSA)、pH值7.4的20 mmol/L磷酸盐缓冲液(PBS)稀释成不同浓度的HBV-LP标准品(0、10、25、50、100和200 ng/mL)。
2.主要仪器与试剂 德国Diasorin公司的ETI-max3000全自动酶免分析仪; HBV-LP酶免试剂盒由北京热景生物技术有限公司提供。
1. HBV-LP标准品吸光度(A)检测 利用上述0 ng/mL标准品将10、25、50、100和200 ng/mL标准品分别稀释成不同浓度的标准品。依据试剂说明书进行编程, 由ETI-max3000全自动酶免分析仪采用酶联免疫吸附试验(ELISA)双抗体夹心法对不同浓度标准品进行双份自动测定A。实验所有操作均严格遵守南昌大学第一附属医院临床免疫实验室标准操作规程(SOP)文件。
2. HBV-LP浓度标准曲线拟合模型的优选原理 利用SPSS曲线估计和MS Excel XP规划求解, 采用最小二乘法拟合HBV-LP标准品实验测定结果, 四参数方程模型的Excel规划求解见图1。以HBV-LP标准品浓度为X, 实验测定的对应A平均值为Y组成一个实验点。将每点的X值代入相应的回归模型, 结合免疫分析回归模型中各参数的生理学含义, 由经验估计方程的参数初值得到Y的拟合值(YΛi)[2~5], 与各点对应测定值Y相减得残差, 求所有点的残差平方和。应用迭代算法, 自动调整方程参数值, 使残差平方和达到最小, 即决定系数(r2)达到最大, 从而求得最优化的各方程终参数[6~8]。根据各回归模型r2的大小来优选血清 HBV-LP浓度标准曲线的最适拟合模型[9]。
采用SPSS 12.0统计软件进行分析, 各回归方程的检验采用F检验, P< 0.05为差异有统计学意义。
HBV感染者血清的感染性与完整病毒(Dane)颗粒的多少和亚病毒颗粒的数量有关。HBV-LP是存在于亚病毒颗粒和Dane颗粒上的外膜蛋白, 其独特的双重拓扑结构和超量表达与病毒复制、肝细胞的直接毒害作用及致癌性、反式激活增强病毒复制作用、上调cccDNA拷贝数作用密切相关, 因此血清HBV-LP浓度的监测对指导HBV感染者的诊治具有重要的临床应用价值。临床实验室定量检测所采用的标准曲线的精度直接影响其检测系统的优化及测定结果的准确度, 目前常用最小二乘法对各离散点进行直线回归来建立标准曲线模型或手工绘制标准曲线。由于检测数据线性化变换会对估计参数的性质产生影响, 如不再具有无偏性, 导致拟合精度偏低, 而用半对数坐标纸手工绘制标准曲线的人为影响因素较大, 因此测定结果误差难以控制。
ELISA分析血清HBV-LP浓度是一个抗原与抗体结合的免疫反应过程, A与浓度之间一般不呈线性关系, 需用五点或七点不同浓度进行定标, 经过各种回归模型拟合才能得出真实反映浓度与A关系的回归方程, 以此绘制定量检测的标准曲线。本研究同时利用了Excel软件的规划求解功能直接对HBV-LP检测数据采用最小二乘法对各种回归模型参数进行迭代算法以最优化解, 发现其拟合效果与SPSS软件的曲线估计一致, 这与文献[10]报道相符, 而且对检测数据未进行线性转化, 避免了因线性化变换对估计参数性质产生的影响, 从而获得了比线性化回归更高的拟合精度。在规划求解的过程中, 可根据散点图趋势和各参数生物学意义设定一定取值范围, 由经验给出参数初值。经过规划求解参数初值的多次尝试给出, 迭代速度与给出的参数初值相关, 但小数点后三位的拟合结果是一致的。因此应用Excel规划求解建立血清HBV-LP浓度标准曲线模型并绘制其拟合标准曲线是一种精确而实用的有效方法, 可直接计算出待测血清HBV-LP浓度, 同时避免了因手工绘制标准曲线的人为因素与繁琐所带来的结果差异。本研究中, HBV-LP标准品检测数据散点图趋势显示在整个取值区间内, A与浓度间的真实关系并非线性, 对A与浓度间进行多种回归模型分析, 发现四参数方程模型、线性模型、对数线性模型、二次多项式模型、三次多项式模型、S模型、Logistic模型的回归方程均有意义(P< 0.001), 以四参数方程模型、二次多项式模型、三次多项式模型、S模型的拟合精度较高, 且以四参数方程模型的拟合精度最佳(r2=0.999 5), 而线性模型、对数线性模型的拟合精度相对较低, 表明四参数方程模型是血清HBV-LP浓度标准曲线的最适拟合模型, 这对临床实验室血清HBV-LP定量检测, 优化实验室检测系统以提高血清HBV-LP定量检测的准确度具有重要的临床指导意义。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|